Table of contents

• Introduction
• What is so special about the 1-dimensional case?
  • Vertices
  • Closed-form formulas
• Going back to optimization methods
  • Fixed-point search: Deterministic Lloyd method
  • Gradient descent
    • Mean-field CLVQ
    • Newton-Raphson method
• Numerical examples
  • Normal distribution
  • Log-Normal distribution
  • Exponential distribution
• References

Introduction

In my previous blog post, I detailed the two main Monte-Carlo simulation-based procedures used to build an optimal Voronoï quantizer of random vectors \(X\) whatever the dimension \(d\).

In this post, I will focus on real valued random variables and explain how to efficiently build optimal quantizers in dimension 1. All the code presented in this blog post is available in the following Github repository: montest/deterministic-methods-optimal-quantization. The main idea is to create an abstract class VoronoiQuantization1D that will contains all generic methods that can be used in order to optimize an optimal quantizer as well as some useful methods in order to compute the distortion, its gradient and hessian. And then implement the methods specific to the distribution of $X$ in the derived classes (e.g NormalVoronoiQuantization, UniformVoronoiQuantization, LogNormalVoronoiQuantization, ExponentialVoronoiQuantization). I will need the following packages:

import scipy
import numpy as np

from typing import Union
from abc import ABC, abstractmethod
from dataclasses import dataclass, field

What is so special about the 1-dimensional case?

In the following figure, I display in red the optimal quantizer of a standard normal distribution of size $N=11$ and the vertices of the cell $C_i(\Gamma_N)$ are represented by black lines on the real axis. The probability associated to the quantizer $x_i^N$ is the integral on the cell $C_i(\Gamma_N)$ of the normal density, as represented in the figure.

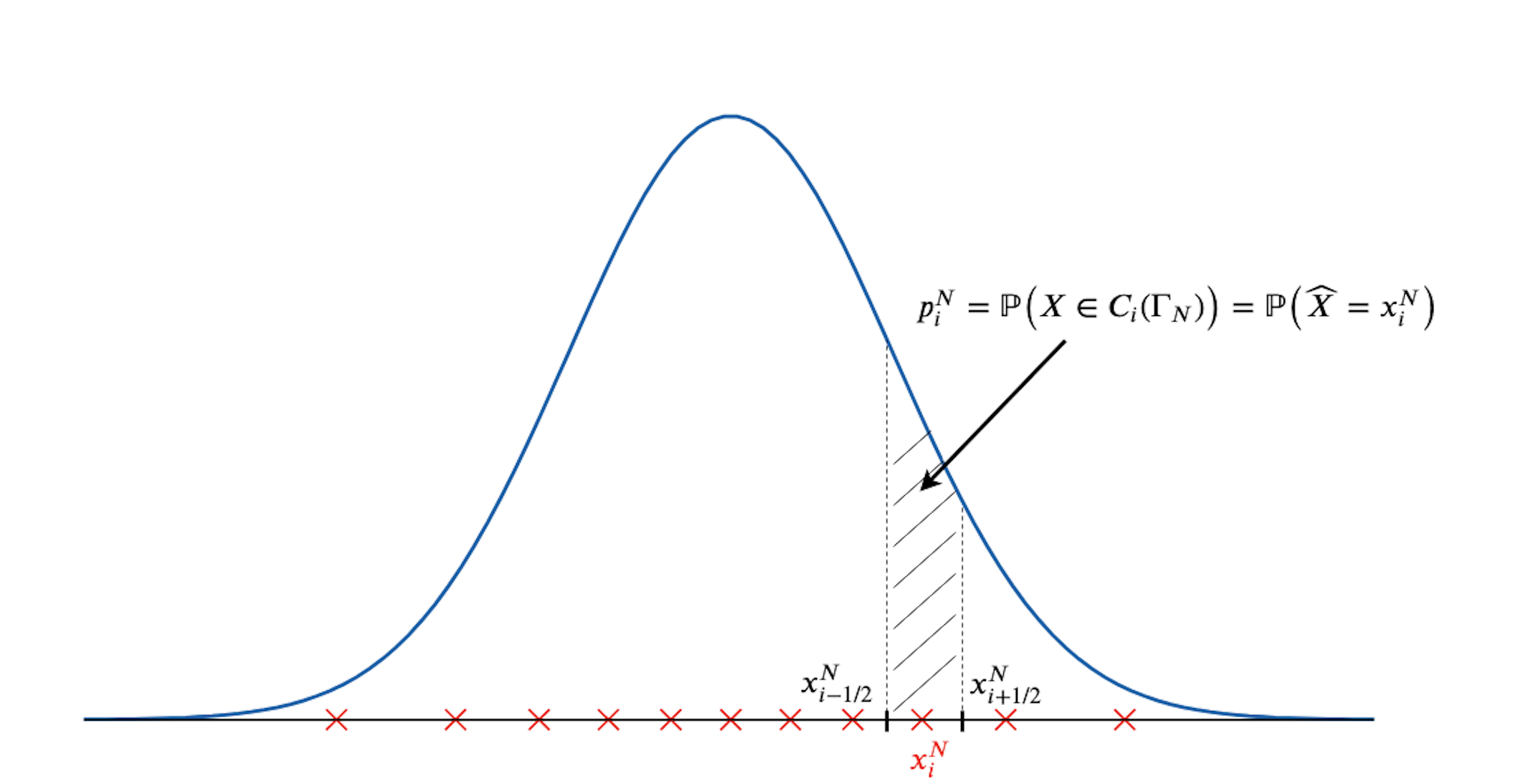
We can notice that the Voronoï cells associated to a quantizer $\widehat X^N$ are intervals in $\mathbb{R}$. Moreover, we can easily compute the coordinate of each vertice (the border of each interval).

Vertices

If we consider that the centroids $(x_i^N)_i$ are ordered: \(x_1^N < x_2^N < \cdots < x_{N-1}^N < x_{N}^N\), then the Voronoï cells are given by

where the vertices $x_{i-1/2}^N$ are defined by

and

In practice, for a list of sorted (from lower to bigger) centroids of size $N$, the vertices can be found using the following method that returns a list of size $N+1$ containing the following: the lower-bound and upper-bound of the support of $X$ and $N-1$ points that are the mid-points between each centroid. For example, for a standard normal distribution, the lower-bound and upper-bound of the support are $- \infty$ and $+ \infty$, respectively. The method get_vertices is defined in the abstract class VoronoiQuantization1D because this method in independent of the random distribution of $X$.

@dataclass
class VoronoiQuantization1D(ABC):

    lower_bound_support: float = field(init=False)
    upper_bound_support: float = field(init=False)

    def get_vertices(self, centroids: np.ndarray) -> np.ndarray:
        vertices = 0.5 * (centroids[1:] + centroids[:-1])
        vertices = np.insert(vertices, 0, self.lower_bound_support)
        vertices = np.append(vertices, self.upper_bound_support)
        return vertices

Closed-form formulas

Let $X$ is a random variable taking values in \(\mathbb{R}\). I remind the expression of the quadratic distortion we wish to minimize in order to build an optimal quantizer $\widehat X^N$. Given an $N$-tuple $x := (x_1^N, \dots, x_N^N) $, the distortion is given by

Now, let us have a look at the gradient’s expression. If we know the density of $X$, then we can devise fast deterministic minimization procedures. Starting from the equation of the gradient of the distortion

it can be rewritten using the expression of the first partial moment and the cumulative distribution function of $X$, yielding

where \(K_{_X}(\cdot)\) and \(F_{_X}(\cdot)\) are, respectively, the first partial moment and the cumulative distribution function of $X$

Compared to the $\mathbb{R}^d$ case, where we needed to draw random samples of $X$ in order to approximate $\nabla \mathcal{Q}_{2,N} (x)$, now, if implementations of \(K_{_X}(\cdot)\) and \(F_{_X}(\cdot)\) exist, then the gradient will be computed very efficiently and the optimal quantization minimization problem will be speed up.

Hence, the following methods can be added to the abstract class VoronoiQuantization1D where

• gradient_distortion computes the quadratic distortion’s gradient for a given quantizer where the list of centroids centroids is sorted,
• cells_expectation computes the expectation of $X$ on each cell using the first partial moment function,
• cells_probability computes the probabilities of $X$ on each cell using the cumulative distribution function (that are the probabilities of the quantizer $\widehat X^N$),
• cdf is an abstract method that needs to be implemented in the derived classes, it is the Cumulative Distribution Function \(F_{_X}(\cdot)\),
• fpm is an abstract method that needs to be implemented in the derived classes, it is the First Partial Moment \(K_{_X}(\cdot)\).

@dataclass
class VoronoiQuantization1D(ABC):

    ...

    def gradient_distortion(self, centroids: np.ndarray) -> np.ndarray:
        vertices = self.get_vertices(centroids)
        to_return = centroids * self.cells_probability(vertices) - self.cells_expectation(vertices)
        return to_return

    def cells_expectation(self, vertices: np.ndarray) -> np.ndarray:
        first_partial_moment = self.fpm(vertices)
        mean_on_each_cell = first_partial_moment[1:] - first_partial_moment[:-1]
        return mean_on_each_cell

    def cells_probability(self, vertices: np.ndarray) -> np.ndarray:
        cumulated_probability = self.cdf(vertices)
        proba_of_each_cell = cumulated_probability[1:] - cumulated_probability[:-1]
        return proba_of_each_cell

    @abstractmethod
    def cdf(self, x: Union[float, np.ndarray]) -> Union[float, np.ndarray]:
        pass

    @abstractmethod
    def fpm(self, x: Union[float, np.ndarray]) -> Union[float, np.ndarray]:
        pass

Remark

The distortion can also be rewritten using \(K_{_X}(\cdot)\) and \(F_{_X}(\cdot)\)

Using this new formula, we can easily compute the distortion using the methods already implemented in VoronoiQuantization1D as long as we know the mean and variance of $X$.

@dataclass
class VoronoiQuantization1D(ABC):

    ...

    mean: float = field(init=False)
    variance: float = field(init=False)

    def distortion(self, centroids: np.ndarray) -> float:
        vertices = self.get_vertices(centroids)

        # First term is variance of random variable
        to_return = self.variance + self.mean ** 2

        # Second term is 2 * \sum_i x_i * E [ X \1_{X \in C_i} ]
        mean_of_each_cell = self.cells_expectation(vertices)
        to_return -= 2. * (centroids * mean_of_each_cell).sum()

        # Third and last term is E [ \widehat X^2 ]
        proba_of_each_cell = self.cells_probability(vertices)
        to_return += (centroids ** 2 * proba_of_each_cell).sum()

        return 0.5 * to_return

In the one dimensional case, we have access to a closed-form formula (or efficient numerical implementation) of the density function, the cumulative distribution function and partial first moment for a lot of random variables. I detail below, for several random variables $X$, \(K_{_X}(\cdot)\), \(F_{_X}(\cdot)\) and \(\varphi_{_X}(\cdot)\), the first partial moment, the cumulative distribution function and the density of $X$, respectively. More formulas can be find in (Montes, 2020) (e.g for Gamma distribution, Non-central $\chi^2(1)$ distribution, Supremum of the Brownian bridge, Symmetric random variable and more). Each example of distribution below is accompanied by its python implementation of the inherited class. The common imports for all classes are given below.

import scipy
import numpy as np

from cmath import inf
from typing import Union
from dataclasses import dataclass, field

from univariate.voronoi_quantization import VoronoiQuantization1D

Click on the bold texts below to expand and see the formulas and details ⤵️

from scipy.stats import norm


@dataclass
class NormalVoronoiQuantization(VoronoiQuantization1D):
    lower_bound_support: float = field(init=False, default=-inf)
    upper_bound_support: float = field(init=False, default=inf)
    mean: float = field(init=False, default=0)
    variance: float = field(init=False, default=1)

    # Probabilty Density Function
    def pdf(self, x: Union[float, np.ndarray]):
        return norm.pdf(x)

    # Cumulative Distribution Function
    def cdf(self, x: Union[float, np.ndarray]):
        return norm.cdf(x)

    # First Partial Moment
    def fpm(self, x: Union[float, np.ndarray]):
        return -self.pdf(x)

    def lr(self, N: int, n: int, max_iter: int):
        a = 2.0 * N
        b = np.pi / float(N * N)
        return a / float(a + b * (n + 1.))

from scipy.stats import lognorm, norm


@dataclass
class LogNormalVoronoiQuantization(VoronoiQuantization1D):
    sigma: float = field(default=1)

    lower_bound_support: float = field(init=False, default=0)
    upper_bound_support: float = field(init=False, default=inf)
    mean: float = field(init=False)
    variance: float = field(init=False)

    def __post_init__(self):
        self.mean = np.exp(0.5 * self.sigma**2)
        self.variance = (np.exp(self.sigma**2)-1.0) * np.exp(self.sigma**2)

    # Probabilty Density Function
    def pdf(self, x: Union[float, np.ndarray]):
        return lognorm.pdf(x, s=self.sigma)

    # Cumulative Distribution Function
    def cdf(self, x: Union[float, np.ndarray]):
        return lognorm.cdf(x, s=self.sigma)

    # First Partial Moment
    def fpm(self, x: Union[float, np.ndarray]):
        return self.mean * norm.cdf(np.log(x) / self.sigma - self.sigma, s=self.sigma)

from scipy.stats import uniform


@dataclass
class UniformVoronoiQuantization(VoronoiQuantization1D):
    lower_bound_support: float = field(init=False, default=0.)
    upper_bound_support: float = field(init=False, default=1.)
    mean: float = field(init=False, default=1.0/2.0)
    variance: float = field(init=False, default=1.0/12.0)

    def optimal_quantization(self, N: int):
        centroids = np.linspace((2.0 - 1.0) / (2.0 * N), (2.0 * N - 1.0) / (2.0 * N), N)
        probabilities = self.cells_probability(self.get_vertices(centroids))
        return centroids, probabilities

    # Probabilty Density Function
    def pdf(self, x: Union[float, np.ndarray]):
        return uniform.pdf(x)

    # Cumulative Distribution Function
    def cdf(self, x: Union[float, np.ndarray]):
        return uniform.cdf(x)

    # First Partial Moment
    def fpm(self, x: Union[float, np.ndarray]):
        return 0.5 * x ** 2

from univariate.voronoi_quantization import VoronoiQuantization1D


@dataclass
class ExponentialVoronoiQuantization(VoronoiQuantization1D):
    lambda_: float = field(default=1)

    lower_bound_support: float = field(init=False, default=0.)
    upper_bound_support: float = field(init=False, default=inf)
    mean: float = field(init=False)
    variance: float = field(init=False)

    def __post_init__(self):
        self.mean = 1./self.lambda_
        self.variance = 1./(self.lambda_ ** 2)

    # Probabilty Density Function
    def pdf(self, x: Union[float, np.ndarray]):
        return self.lambda_ * np.exp(-self.lambda_*x)

    # Cumulative Distribution Function
    def cdf(self, x: Union[float, np.ndarray]):
        return 1. - np.exp(-self.lambda_*x)

    # First Partial Moment
    def fpm(self, x: Union[float, np.ndarray]):
        to_return = - np.exp(-self.lambda_*x)*(x+self.mean) + self.mean
        if type(x) == float and x == inf:
            to_return = self.mean
        # If x is an array then it is supposed to be sorted hence if there is an inf value, it is the last value and it
        # should appear only once in the case of optimal quantization.
        if type(x) == np.ndarray and x[-1] == inf:
            to_return[-1] = self.mean
        return to_return

Going back to optimization methods

Fixed-point search: Deterministic Lloyd method

In my previous blog post, I derived a fixed-point problem from Equation \ref{eq:grad_dist_deter}, such that

where

which in the one-dimensional case can be rewritten using \(K_{_X}\) and \(F_{_X}\)

Hence, from this equality, we can write the following fixed-point search algorithm. This method is known as the deterministic Lloyd method. The Lloyd method was first devised by Lloyd in (Lloyd, 1982). Let \(\Lambda : \mathbb{R}^N \mapsto \mathbb{R}^N\) such that \(\Lambda = (\Lambda_i)_{1 \leq i \leq N}\), the Lloyd method with initial condition \(x^0\) is defined as follows

where $x^{[n]}$ is the quantizer obtained after $n$ iterations of the algorithm. The pseudo-algorithm of the Lloyd method written on the vector \(x\) starting from a given quantizer $x^{0}$.

Using this formulation, we can easily implement a deterministic version of the Lloyd algorithm deterministic_lloyd_method using the methods already implemented in VoronoiQuantization1D that takes as input centroids, a list of centroids of size $N$ sorted by values (from lower to bigger) and nbr_iterations, the number of fixed point iterations we want to do.

@dataclass
class VoronoiQuantization1D(ABC):

    ...

    def deterministic_lloyd_method(self, centroids: np.ndarray, nbr_iterations: int):

        for i in range(nbr_iterations):
            vertices = self.get_vertices(centroids)
            mean_of_each_cell = self.cells_expectation(vertices)
            proba_of_each_cell = self.cells_probability(vertices)
            centroids = mean_of_each_cell / proba_of_each_cell

        probabilities = self.cells_probability(self.get_vertices(centroids))
        return centroids, probabilities

Remark

An interesting fact about the Lloyd method, is that each step of the fixed-point search preserve the sorting property of centroids (which is not always the case for the following algorithms).

Gradient descent

Another approach for building an optimal quantizer consists in minimizing directly Equation \ref{eq:distortion} using a gradient descent. I detail two algorithms below: Mean-field CLVQ and Newton-Raphson.

Mean-field CLVQ

The first idea is to use a first-order gradient descent. This is the deterministic or batch version of the Competitive Learning Vector Quantization (CLVQ) algorithm detailed in my previous blog post, which is a stochastic gradient descent introduced for the cases where we cannot numerically compute the gradient. In the one dimensional case, the gradient is easily computable using the expression of \(F_{_X}\) and \(K_{_X}\), as detailed in Equation \ref{eq:grad_dist_deter} hence a gradient descent is applied directly on the distortion. Starting from a given initial condition \(x^0\), the quantizer after \(n+1\) iterations is given by

where \(\gamma_{n+1} \in (0,1)\) is either taken constant (\(\gamma_{n+1} = \gamma\)) or updated at each step using a line search (see (Bonnans et al., 2006; Swann, 1969)) or using the Barzilai–Borwein method (see (Barzilai & Borwein, 1988)).

I give below the Python implementation of the method mean_field_clvq_method that takes as input centroids, a list of sorted centroids and nbr_iterations, the number of gradient descend. By default, we chose lr to be equal to $0.1$ but more advanced learning rates can be chosen (eg. see the implementation of lr in the class NormalVoronoiQuantization where the origin of this function can be find in (Pagès, 2018) or decreasing learning rates with a warm-up phase could also be considered).

@dataclass
class VoronoiQuantization1D(ABC):

    ...

    def mean_field_clvq_method(self, centroids: np.ndarray, nbr_iterations: int):

        for i in range(nbr_iterations):
            gradient = self.gradient_distortion(centroids)
            lr = self.lr(len(centroids), i, nbr_iterations)
            centroids = centroids - lr * gradient
            centroids.sort()

        probabilities = self.cells_probability(self.get_vertices(centroids))
        return centroids, probabilities

    def lr(self, N: int, n: int, max_iter):
        return 0.1

Newton-Raphson method

One can improve the rate of convergence of the algorithm defined above using a second-order gradient descent where the step \(\gamma_{n+1}\) is chosen optimally at each step and is set as the inverse of the Hessian matrix of the distortion function. This method is known as the Newton-Raphson method and was first use in the case of optimal quantization in (Pagès & Printems, 2003). Again, starting from a initial condition \(x^0\) at step \(0\), we have

with $\nabla^2 \mathcal{Q}_{2,N} (x)$ the Hessian matrix for $x = (x_1, \dots, x_N)$

The Hessian matrix is tridiagonal and since we have access to \(X\)’s density and cumulative distribution functions, each component of the matrix can be computed efficiently with the following expression

The implementation of the method hessian_distortion, that for given list of centroids as input returns an array of size (N, N) containing the hessian matrix is given below. The abstract method pdf is defined in the inherited classes (eg, see the implementation of NormalVoronoiQuantization).

@dataclass
class VoronoiQuantization1D(ABC):

    ...

    def hessian_distortion(self, centroids: np.ndarray):
        N = len(centroids)
        result = np.zeros((N, N))
        vertices = self.get_vertices(centroids)
        proba_of_each_cell = self.cells_probability(vertices)
        tempDens = self.pdf(vertices)

        a = 0.0
        for i in range(N - 1):
            result[i, i] = 2 * proba_of_each_cell[i] - tempDens[i] * a
            a = (centroids[i + 1] - centroids[i]) * 0.5
            result[i, i] -= tempDens[i + 1] * a
            result[i, i + 1] = - a * tempDens[i + 1]
            result[i + 1, i] = result[i, i + 1]
        result[N - 1, N - 1] = 2 * proba_of_each_cell[N - 1] - tempDens[N - 1] * a
        return result

    @abstractmethod
    def pdf(self, x: Union[float, np.ndarray]) -> Union[float, np.ndarray]:
        pass

The Python code of the Newton-Raphson method is detailed below, where in place of computing the inverse of the Hessian matrix, I solve the following linear system: I search for $u \in \mathbb{R}^N$ solution of

where \(H = \nabla^2 \mathcal{Q}_{2,N} (x)\) and \(G=\nabla \mathcal{Q}_{2,N} (x)\).

@dataclass
class VoronoiQuantization1D(ABC):

    ...

    def newton_raphson_method(self, centroids: np.ndarray, nbr_iterations: int):

        for i in range(nbr_iterations):
            hessian = self.hessian_distortion(centroids)
            gradient = self.gradient_distortion(centroids)
            inv_hessian_dot_grad = scipy.linalg.solve(hessian, gradient, assume_a='sym')
            centroids = centroids - inv_hessian_dot_grad
            centroids.sort()  # we sort the centroids because Newton-Raphson does not always preserve the order

        probabilities = self.cells_probability(self.get_vertices(centroids))
        return centroids, probabilities

The problem with the Newton-Raphson algorithm is that it suffers from high instability when the Hessian is almost non-invertible. It often arises when we wish to build optimal quantizers for high values of $N$. Moreover, when $N$ is large, even though Newton-Raphson algorithm needs few iterations to converge (when it converges), each iteration requires a lengthy amount of time because of the space needed in memory in order to store the hessian matrix and solve the linear problem (find $u$ in Equation \ref{eq:linear_syst_hessian}) which results in slow convergence.

Numerical examples

In this part, I test the previously detailed algorithms in order to build optimal quantizers for different distributions, namely: Normal, Log-Normal and Exponential. I plot the distortion as a function of the number of iteration of a given optimization method. mfclvq corresponds to the Mean-Field CLQV gradient descent, lloyd to the Lloyd method and nr to the Newton-Raphson gradient descent. For each distribution, I show the convergence for 2 sizes of grid: $N=10$ and $N=50$.

Several remarks can be made on the following figures:

• First, one can notice that for $N=50$, I do not plot the results for the Newton-Raphson. It is because of the numerical instability induced by the “almost” non-invertible Hessian matrix. I will detail on future blog-posts (see also Chapter 1 in (Montes, 2020)) how to fix this issue and still use the Hessian matrix when we wish to optimize optimal quantizers. However, in the case $N=10$, when the inverse of the Hessian is not ill-defined, we can notice that the Newton-Raphson algorithm converges very quickly and beats all the other methods.
• Second, in the normal distribution case, mfclvq converges very quickly even with higher values of $N$. This due to a well chosen learning rate (see (Pagès & Printems, 2003)) where the authors wish to taken into account the mode of the normal distribution. So, we can notice than the choice of the learning rate for the gradient descent is crucial and it can lead to really fast convergence as very slow (see for example the log normal distribution where we chose a constant learning rate equal to $0.1$).
• Finally, the Lloyd method gives consistent and very good results (it need less than a 100 iterations in order to reach the precision of the Newton-Raphson algorithm) for all 3 distributions and the 2 quantizer’s sizes making the Lloyd algorithm a very good and reliable method.

Normal distribution

Log-Normal distribution

Exponential distribution

References

1. Montes, T. (2020). Numerical methods by optimal quantization in finance [PhD thesis]. Sorbonne université.
2. Pagès, G. (2018). Numerical Probability: An Introduction with Applications to Finance. Springer. https://doi.org/10.1007/978-3-319-90276-0
3. Callegaro, G., Fiorin, L., & Grasselli, M. (2019). Quantization meets Fourier: a new technology for pricing options. Annals of Operations Research, 282(1-2), 59–86.
4. Lloyd, S. (1982). Least squares quantization in PCM. IEEE Transactions on Information Theory, 28(2), 129–137.
5. Bonnans, J.-F., Gilbert, J. C., Lemaréchal, C., & Sagastizábal, C. A. (2006). Numerical optimization: theoretical and practical aspects. Springer Science & Business Media.
6. Swann, W. H. (1969). A survey of non-linear optimization techniques. FEBS Letters, 2(S1), S39–S55.
7. Barzilai, J., & Borwein, J. M. (1988). Two-point step size gradient methods. IMA Journal of Numerical Analysis, 8(1), 141–148.
8. Pagès, G., & Printems, J. (2003). Optimal quadratic quantization for numerics: the Gaussian case. Monte Carlo Methods and Applications, 9(2), 135–165.