Optimal Quantization with PyTorch - Part 1: Implementation of Stochastic Lloyd Method
Published:
Table of contents
Introduction
In this post, I present a PyTorch implementation of the stochastic version of the Lloyd algorithm, aka K-Means, in order to build Optimal Quantizers of $X$, a random variable of dimension one. The use of PyTorch allows me perform all the numerical computations on GPU and drastically increase the speed of the algorithm. I compare the implementation I made in numpy in a previous blog post with the PyTorch version and study how it scales.
All the codes presented in this blog post are available in the following Github repository: montest/stochastic-methods-optimal-quantization
Short Reminder
In this part, I quickly remind how to build an optimal quantizer using the Monte-Carlo simulation-based Lloyd procedure with a focus on the $1$-dimensional case. To get more background on the notations and the theory, do not hesitate to check-out my previous blog articles on Stochastic and Deterministic methods for building optimal quantizers.
Voronoï Quantization in dimension 1
Given a quantizer of size N: \(\Gamma_N = \big\{ x_{1}^{N}, \dots , x_{N}^{N} \big\}\) where $x_i^{N}$ are the centroids. Keeping in mind that we are in the $1$-dimensional, if we consider that the centroids $(x_i^{N})_i$ are ordered: \(x_1^{N} < x_2^{N} < \cdots < x_{N-1}^{N} < x_{N}^{N}\), then the Voronoï cells $C_i (\Gamma_N)$ are intervals in $\mathbb{R}$ and are defined by
\[C_i ( \Gamma_N ) = \left\{ \begin{aligned} & \big( x_{i - 1/2}^N , x_{i + 1/2}^N \big] &\qquad i = 1, \dots, N-1 \\ & \big( x_{i - 1/2}^N , x_{i + 1/2}^N \big) & i = N \end{aligned} \right.\]where the vertices $x_{i-1/2}^N$ are defined by
\[\forall i = 2, \dots, N, \qquad x_{i-1/2}^N := \frac{x_{i-1}^N + x_i^N}{2}\]and
\[x_{1/2}^N := \textrm{inf} (\textrm{supp} (\mathbb{P}_{_{X}})) \, \textrm{ and } \, x_{N+1/2}^N := \textrm{sup} (\textrm{supp} (\mathbb{P}_{_{X}})).\]Now, let $X$ be a random variable, a Voronoï quantization of $X$ by $\Gamma_{N}$, $\widehat X^N$, is defined as nearest neighbor projection of $X$ onto $\Gamma_{N}$ associated to a Voronoï partition $\big( C_{i} (\Gamma_{N}) \big)_{i =1, \dots, N}$ for the euclidean norm
\[\widehat X^N := \textrm{Proj}_{\Gamma_{N}} (X) = \sum_{i = 1}^N x_i^N \mathbb{1}_{X \in C_{i} (\Gamma_N) }\]and its associated probabilities, also called weights, are given by
\[\mathbb{P} \big( \widehat X^N = x_i^N \big) = \mathbb{P}_{_{X}} \big( C_{i} (\Gamma_N) \big) = \mathbb{P} \big( X \in C_{i} (\Gamma_N) \big).\]Optimal quantization
In order to build an optimal quantizer of $X$, we are looking for the best approximation of $X$ in the sense that we want to find the quantizer $\widehat X^N$ which is the \(\arg \min\) of the quadratic distortion function at level $N$ induced by an $N$-tuple $x := (x_1^N, \dots, x_N^N)$ given by
\[\mathcal{Q}_{2,N} : x \longmapsto \frac{1}{2} \Vert X - \widehat X^N \Vert_{_2}^2 .\]Randomized Lloyd algorithm
One of the first method deployed in order to build optimal quantizers was the Lloyd method, which is a fixed-point search algorithm. Let $x^{[n]}$ be the quantizer of size $N$ obtained after $n$ iterations, the Randomized Lloyd method with initial condition $x^0$ is defined as follows
\[x^{[n+1]} = \Lambda^M \big( x^{[n]} \big),\]where
\[\Lambda_i^M ( x ) = \frac{\displaystyle \sum_{m=1}^M \xi_m \mathbb{1}_{ \big\{ \textrm{Proj}_{\Gamma_N} (\xi_m) = x_i^N \big\} } }{\displaystyle \sum_{m=1}^M \mathbb{1}_{ \big\{ \textrm{Proj}_{\Gamma_N} (\xi_m) = x_i^N \big\} } }, % \qquad \mbox{with} \qquad \Gamma_N = \{ x_1^N, \dots, x_N^N \}\]with $\xi_1, \dots, \xi_M$ be independent copies of $X$.
Numpy Implementation
I detail below a Python code example using numpy, which is an optimized version of the code I detailed in my previous blog post of the randomized Lloyd method. It applies nbr_iter iterations of the fixed point function in order to build an optimal quantizer of a gaussian random variable where you can select N the size of the optimal quantizer, M the number of sample you want to generate.
import numpy as np
from tqdm import trange
def lloyd_method_dim_1(N: int, M: int, nbr_iter: int, seed: int = 0):
"""
Apply `nbr_iter` iterations of the Randomized Lloyd algorithm in order to build an optimal quantizer of size `N`
for a Gaussian random variable. This implementation is done using numpy.
N: number of centroids
M: number of samples to generate
nbr_iter: number of iterations of fixed point search
seed: numpy seed for reproducibility
Returns: centroids, probabilities associated to each centroid and distortion
"""
np.random.seed(seed) # Set seed in order to be able to reproduce the results
# Draw M samples of gaussian variable
xs = np.random.normal(0, 1, size=M)
# Initialize the Voronoi Quantizer randomly and sort it
centroids = np.random.normal(0, 1, size=N)
centroids.sort(axis=0)
for step in trange(nbr_iter, desc=f'Lloyd method - N: {N} - M: {M} - seed: {seed} (numpy)'):
# Compute the vertices that separate the centroids
vertices = 0.5 * (centroids[:-1] + centroids[1:])
# Find the index of the centroid that is closest to each sample
index_closest_centroid = np.sum(xs[:, None] >= vertices[None, :], axis=1)
# Compute the new quantization levels as the mean of the samples assigned to each level
centroids = np.array([np.mean(xs[index_closest_centroid == i], axis=0) for i in range(N)])
if any(np.isnan(centroids)):
break
# Find the index of the centroid that is closest to each sample
vertices = 0.5 * (centroids[:-1] + centroids[1:])
index_closest_centroid = np.sum(xs[:, None] >= vertices[None, :], axis=1)
# Compute the probability of each centroid
probabilities = np.bincount(index_closest_centroid) / float(M)
# Compute the final distortion between the samples and the quantizer
distortion = ((xs - centroids[index_closest_centroid]) ** 2).sum() / float(2 * M)
return centroids, probabilities, distortion
The advantage of this optimized version is twofold. First, it drastically reduces the computation time in order to build an optimal quantizer. Second, this new version is written is a more pythonic way compared to the one detailed in my previous article. This simplifies greatly the conversion of this code to PyTorch, as you can see in the next section.
PyTorch Implementation
Using the numpy code version written above, we can easily implement the Lloyd algorithm in PyTorch. The main difference is the usage of torch.no_grad() in order to make sure we don’t accumulate the gradients in the tensors and before applying the fixed point iterator, we send the centroids and the samples to the chosen device: cpu or cuda.
As above, lloyd_method_dim_1_pytorch applies nbr_iter iterations of the fixed point function in order to build an optimal quantizer of a gaussian random variable where you can select N the size of the optimal quantizer, M the number of sample you want to generate.
import torch
from tqdm import trange
def lloyd_method_dim_1_pytorch(N: int, M: int, nbr_iter: int, device: str, seed: int = 0):
"""
Apply `nbr_iter` iterations of the Randomized Lloyd algorithm in order to build an optimal quantizer of size `N`
for a Gaussian random variable. This implementation is done using torch.
N: number of centroids
M: number of samples to generate
nbr_iter: number of iterations of fixed point search
device: device on which perform the computations: "cuda" or "cpu"
seed: torch seed for reproducibility
Returns: centroids, probabilities associated to each centroid and distortion
"""
torch.manual_seed(seed=seed) # Set seed in order to be able to reproduce the results
with torch.no_grad():
# Draw M samples of gaussian variable
xs = torch.randn(M)
# xs = torch.tensor(torch.randn(M), dtype=torch.float32)
xs = xs.to(device) # send samples to correct device
# Initialize the Voronoi Quantizer randomly
centroids = torch.randn(N)
centroids, index = centroids.sort()
centroids = centroids.to(device) # send centroids to correct device
for step in trange(nbr_iter, desc=f'Lloyd method - N: {N} - M: {M} - seed: {seed} (pytorch: {device})'):
# Compute the vertices that separate the centroids
vertices = 0.5 * (centroids[:-1] + centroids[1:])
# Find the index of the centroid that is closest to each sample
index_closest_centroid = torch.sum(xs[:, None] >= vertices[None, :], dim=1).long()
# Compute the new quantization levels as the mean of the samples assigned to each level
centroids = torch.tensor([torch.mean(xs[index_closest_centroid == i]) for i in range(N)]).to(device)
if torch.isnan(centroids).any():
break
# Find the index of the centroid that is closest to each sample
vertices = 0.5 * (centroids[:-1] + centroids[1:])
index_closest_centroid = torch.sum(xs[:, None] >= vertices[None, :], dim=1).long()
# Compute the probability of each centroid
probabilities = torch.bincount(index_closest_centroid).to('cpu').numpy()/float(M)
# Compute the final distortion between the samples and the quantizer
distortion = torch.sum(torch.pow(xs - centroids[index_closest_centroid], 2)).item() / float(2 * M)
return centroids.to('cpu').numpy(), probabilities, distortion
Numerical experiments
Now, I compare the average elapsed time of a fixed-point search iteration of the previous two algorithms. I analyze the computation time of the algorithms for different sample size (M), grid size (N) and devices for the PyTorch implementation.
All the tests were conducted on Google Cloud Platform on an instance n1-standard-4 with 4 cores, 16 Go of RAM and a NVIDIA T4 GPU.
In order to reproduce those results, you can run the script benchmark/run_lloyd.py in the GitHub repository montest/stochastic-methods-optimal-quantization.
In the left graph, I display, for each method, the average time of an iteration for several values of N.
In the right graph, I plot, for each N, the ratio between the average time for each method and the average time spent by PyTorch implementation using cuda.
We can notice that when it comes to cpu-only computations, numpy is a better choice than PyTorch. However, when using the GPU, we notice that the PyTorch + cuda version is up to 20 times faster than the numpy implementation. And this is even more noticeable when we increase the sample size.







 In this post, I present several PyTorch implementations of the Competitive Learning Vector Quantization algorithm (CLVQ) in order to build Optimal Quantizers of $X$, a random variable of dimension one. In my previous blog post, the use of PyTorch for Lloyd allowed me to perform all the numerical computations on GPU and drastically increase the speed of the algorithm. However, in this article, we do not observe the same behavior, this pytorch implementation is slower than the numpy one. Moreover, I also take advantage of the autograd implementation in PyTorch allowing me to make use of all the optimizers in
In this post, I present several PyTorch implementations of the Competitive Learning Vector Quantization algorithm (CLVQ) in order to build Optimal Quantizers of $X$, a random variable of dimension one. In my previous blog post, the use of PyTorch for Lloyd allowed me to perform all the numerical computations on GPU and drastically increase the speed of the algorithm. However, in this article, we do not observe the same behavior, this pytorch implementation is slower than the numpy one. Moreover, I also take advantage of the autograd implementation in PyTorch allowing me to make use of all the optimizers in 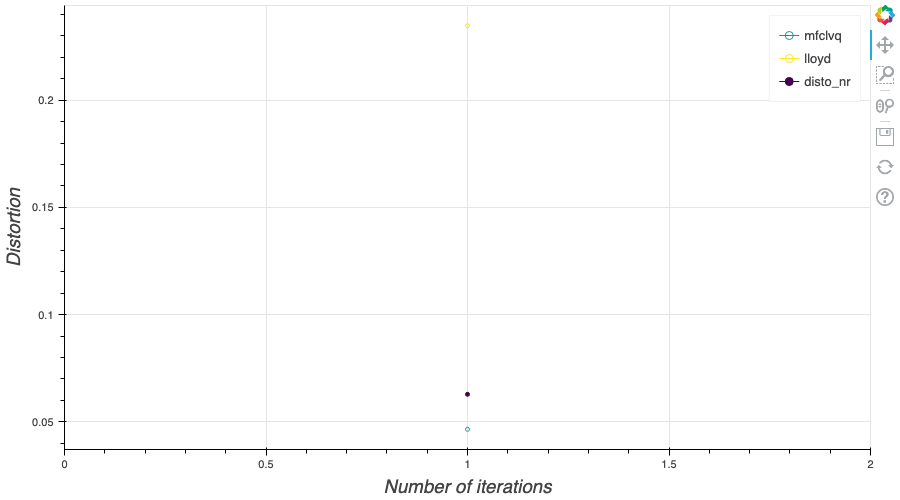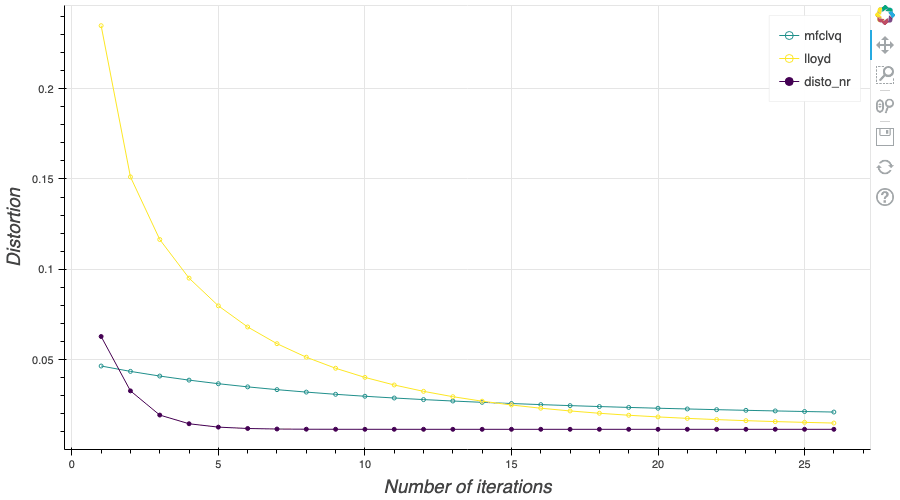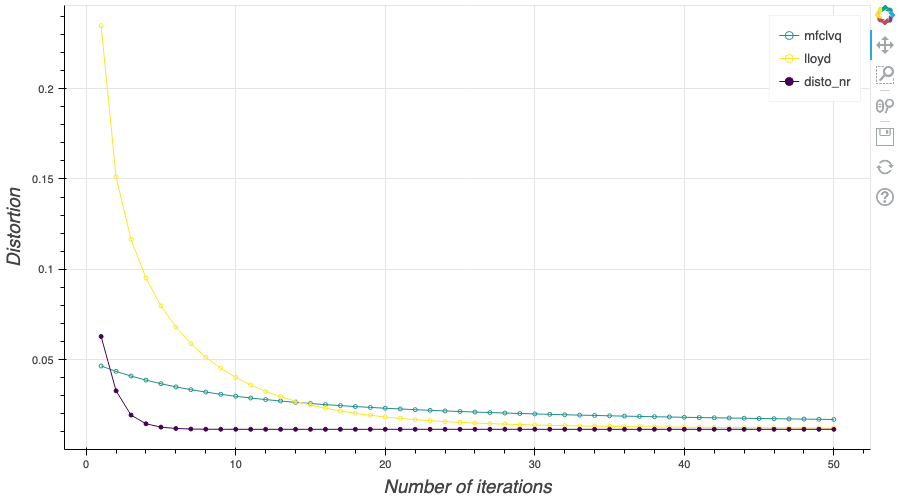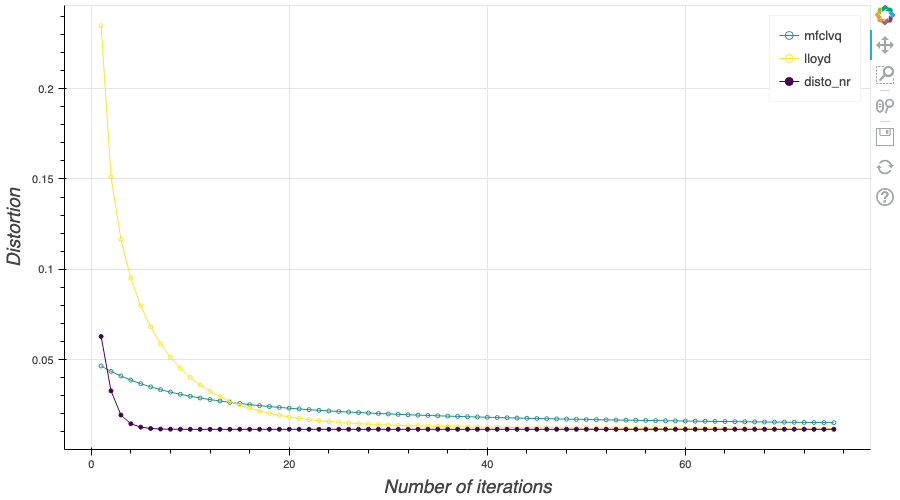 In my previous blog post, I detailed the methods used to build an optimal Voronoï quantizer of random vectors \(X\) whatever the dimension \(d\). In this post, I will focus on real valued random variables and present faster methods for dimension $1$.
In my previous blog post, I detailed the methods used to build an optimal Voronoï quantizer of random vectors \(X\) whatever the dimension \(d\). In this post, I will focus on real valued random variables and present faster methods for dimension $1$. In this post, I remind what is quadratic optimal quantizations. Then, I explain the two algorithms that were first devised in order to build an optimal quantization of a random vector $X$, namely: the fixed-point search called Lloyd method and the stochastic gradient descent known as Competitive Learning Vector Quantization (CLVQ).
In this post, I remind what is quadratic optimal quantizations. Then, I explain the two algorithms that were first devised in order to build an optimal quantization of a random vector $X$, namely: the fixed-point search called Lloyd method and the stochastic gradient descent known as Competitive Learning Vector Quantization (CLVQ).