Optimal Quantization with PyTorch - Part 2: Implementation of Stochastic Gradient Descent
Published:
Table of contents
- Introduction
- Short Reminder
- Numpy Implementation
- PyTorch Implementation
- Numerical experiments
- Conclusion
Introduction
In this post, I present several PyTorch implementations of the Competitive Learning Vector Quantization algorithm (CLVQ) in order to build Optimal Quantizers of $X$, a random variable of dimension one. In my previous blog post, the use of PyTorch allowed me to perform all the numerical computations on GPU and drastically increase the speed of the algorithm. However, in this article, we do not observe the same behavior, this pytorch implementation is slower than the numpy one. Moreover, I also take advantage of the autograd implementation in PyTorch allowing me to make use of all the optimizers in torch.optim. Again, this implementation does not speed up the optimization (on the contrary) but it opens the door to other use of the autograd algorithm with other methods (e.g. in the deterministic case). I compare the implementation I made in numpy in a previous blog post with the PyTorch version and study how it scales. Moreover, I explore the use of autograd in PyTorch.
All the codes presented in this blog post are available in the following Github repository: montest/stochastic-methods-optimal-quantization
Short Reminder
Using the notations I used in my previous articles (1, 2 and 3), I first remind the expression of the minimization problem we want to solve in order to build an optimal quantizer. Then, I detail the expression of the gradient of the distortion and, finally, the stochastic version of CLVQ algorithm used to build optimal quantizers.
Distortion function
In order to build an optimal quantizer of $X$, we are looking for the best approximation of $X$ in the sense that we want to find the quantizer $\widehat X^N$ which is the \(\arg \min\) of the quadratic distortion function at level $N$ induced by an $N$-tuple $x := (x_1^N, \dots, x_N^N)$
\[\textrm{arg min}_{(\mathbb{R})^N} \mathcal{Q}_{2,N},\]where \(\mathcal{Q}_{2,N}\) given by
\[\mathcal{Q}_{2,N} : x \longmapsto \frac{1}{2} \Vert X - \widehat X^N \Vert_{_2}^2 .\]Gradient of the distortion function
The \(\arg \min\) of the distortion can be found by differentiating the distortion function \(\mathcal{Q}_{2,N}\). The gradient \(\nabla \mathcal{Q}_{2,N}\) is given by
\[\nabla \mathcal{Q}_{2,N} (x) = \bigg[ \int_{C_i (\Gamma_N)} (x_i^N - \xi ) \mathbb{P}_{_{X}} (d \xi) \bigg]_{i = 1, \dots, N } = \Big[ \mathbb{E}\big[ \mathbb{1}_{X \in C_i (\Gamma_N)} ( x_i^N - X ) \big] \Big]_{i = 1, \dots, N }.\]Stochastic Competitive Learning Vector Quantization algorithm
Then, using the gradient, one can use a Stochastic Gradient Descent, also called the CLVQ algorithm in order to build an optimal quantizer. Let $x^{[n]}$ be the quantizer of size $N$ obtained after $n$ iterations, the Stochastic CLVQ method with initial condition $x^0$ is defined as follows
\[x^{[n+1]} = x^{[n]} - \gamma_{n+1} \nabla \textit{q}_{2,N} (x^{[n]}, \xi_{n+1})\]with $\xi_1, \dots, \xi_n, \dots$ a sequence of independent copies of $X$ and
\[\nabla \textit{q}_{2,N} (x^{[n]}, \xi_{n+1}) = \Big( \mathbb{1}_{\xi_{n+1} \in C_i (\Gamma_N)} ( x_i^{[n]} - \xi_{n+1} ) \Big)_{1 \leq i \leq N}.\]Numpy Implementation
I detail below a Python code example using numpy, which is an optimized version of the code I detailed in my previous blog post of the stochastic CLVQ. It samples M samples of the distribution you want to quantize. Then it applies num_epochs times M gradient descent steps in order to build an optimal quantizer of size N.
import numpy as np
from tqdm import trange
from utils import get_probabilities_and_distortion
def lr(N: int, n: int):
a = 4.0 * N
b = np.pi ** 2 / float(N * N)
return a / float(a + b * (n+1.))
def clvq_method_dim_1(N: int, M: int, num_epochs: int, seed: int = 0):
"""
Apply `nbr_iter` iterations of the Competitive Learning Vector Quantization algorithm in order to build an optimal
quantizer of size `N` for a Gaussian random variable. This implementation is done using numpy.
N: number of centroids
M: number of samples to generate
num_epochs: number of epochs of fixed point search
seed: numpy seed for reproducibility
Returns: centroids, probabilities associated to each centroid and distortion
"""
np.random.seed(seed) # Set seed in order to be able to reproduce the results
# Draw M samples of gaussian variable
xs = np.random.normal(0, 1, size=M)
# Initialize the Voronoi Quantizer randomly and sort it
centroids = np.random.normal(0, 1, size=N)
centroids.sort(axis=0)
with trange(num_epochs, desc=f'CLVQ method - N: {N} - M: {M} - seed: {seed} (numpy)') as epochs:
for epoch in epochs:
for step in range(M):
# Compute the vertices that separate the centroids
vertices = 0.5 * (centroids[:-1] + centroids[1:])
# Find the index of the centroid that is closest to each sample
index_closest_centroid = np.sum(xs[step, None] >= vertices[None, :])
gamma_n = lr(N, epoch*M + step)
# Update the closest centroid using the local gradient
centroids[index_closest_centroid] = centroids[index_closest_centroid] - gamma_n * (centroids[index_closest_centroid] - xs[step])
probabilities, distortion = get_probabilities_and_distortion(centroids, xs)
return centroids, probabilities, distortion
Compared to the version presented in a previous blog post, I reuse the same M samples each time. and do not resample for each epoch, Moreover, the probabilities and the distortion are computed at the end using the following method get_probabilities_and_distortion where centroids are the centroids and xs are the M samples.
import torch
import numpy as np
from typing import Union
def get_probabilities_and_distortion(centroids: Union[np.ndarray, torch.tensor], xs: Union[np.ndarray, torch.tensor]):
"""
Compute the probabilities and the distortion associated to `centroids` using the samples `xs`
centroids: centroids of size `N`
xs: `M` samples to use in order to compute the probabilities and the distortion
Returns: probabilities associated to each centroid and distortion
"""
centroids_ = centroids.clone().detach() if torch.is_tensor(centroids) else torch.tensor(centroids)
xs_ = xs.clone().detach() if torch.is_tensor(xs) else torch.tensor(xs)
M = len(xs_)
vertices = 0.5 * (centroids_[:-1] + centroids_[1:])
index_closest_centroid = torch.sum(xs_[:, None] >= vertices[None, :], dim=1).long()
# Compute the probability of each centroid
probabilities = torch.bincount(index_closest_centroid).to('cpu').numpy() / float(M)
# Compute the final distortion between the samples and the quantizer
distortion = torch.sum(torch.pow(xs_ - centroids_[index_closest_centroid], 2)).item() / float(2 * M)
return probabilities, distortion
PyTorch Implementation
Standard implementation
Again, as in my previous blog post, using the numpy code version written above, we can easily implement the CLVQ algorithm in PyTorch. In clvq_method_dim_1_pytorch, I used the same variables and notations as in the numpy implementation. There is one extra variable device that should have one of the two values cpu or cuda that defines where the computations will be done.
import torch
from tqdm import trange
from utils import get_probabilities_and_distortion
def lr(N: int, n: int):
a = 4.0 * N
b = torch.pi ** 2 / float(N * N)
return a / float(a + b * (n+1.))
def clvq_method_dim_1_pytorch(N: int, M: int, num_epochs: int, device: str, seed: int = 0):
"""
Apply `nbr_iter` iterations of the Competitive Learning Vector Quantization algorithm in order to build an optimal
quantizer of size `N` for a Gaussian random variable. This implementation is done using torch.
N: number of centroids
M: number of samples to generate
num_epochs: number of epochs of fixed point search
device: device on which perform the computations: "cuda" or "cpu"
seed: numpy seed for reproducibility
Returns: centroids, probabilities associated to each centroid and distortion
"""
torch.manual_seed(seed=seed) # Set seed in order to be able to reproduce the results
with torch.no_grad():
# Draw M samples of gaussian variable
xs = torch.randn(M)
xs = xs.to(device) # send samples to correct device
# Initialize the Voronoi Quantizer randomly and sort it
centroids = torch.randn(N)
centroids, index = centroids.sort()
centroids = centroids.to(device) # send centroids to correct device
with trange(num_epochs, desc=f'CLVQ method - N: {N} - M: {M} - seed: {seed} (pytorch: {device})') as epochs:
for epoch in epochs:
for step in range(M):
# Compute the vertices that separate the centroids
vertices = 0.5 * (centroids[:-1] + centroids[1:])
# Find the index of the centroid that is closest to each sample
index_closest_centroid = torch.sum(xs[step, None] >= vertices[None, :]).long()
gamma_n = 1e-2
# gamma_n = lr(N, epoch*M + step)
# Update the closest centroid using the local gradient
centroids[index_closest_centroid] = centroids[index_closest_centroid] - gamma_n * (centroids[index_closest_centroid] - xs[step])
probabilities, distortion = get_probabilities_and_distortion(centroids, xs)
return centroids.to('cpu').numpy(), probabilities, distortion
Remark
Now that the converted the numpy implementation into PyTorch, we can try to take advantage of another big feature of PyTorch, which is
autograd. It is described as follow in PyTorch documentation:
PyTorch’s Autograd feature is part of what make PyTorch flexible and fast for building machine learning projects. It allows for the rapid and easy computation of multiple partial derivatives (also referred to as gradients) over a complex computation. This operation is central to backpropagation-based neural network learning.
The power of autograd comes from the fact that it traces your computation dynamically at runtime, meaning that if your model has decision branches, or loops whose lengths are not known until runtime, the computation will still be traced correctly, and you’ll get correct gradients to drive learning. This, combined with the fact that your models are built in Python, offers far more flexibility than frameworks that rely on static analysis of a more rigidly-structured model for computing gradients.
This will allows us to not compute the gradient by hand and most importantly to take advantage of all the optimizers already implemented in
torch.optimsuch as SGD with momentum or ADAM.
Gradient descent with the use of autograd
First, we define Quantizer that inherit from torch.nn.Module that, at initialization, creates a random quantizer of size N and set self.centroids as parameters for which we need to compute the gradient using .requires_grad_(True).
from torch import nn
class Quantizer(nn.Module):
def __init__(self, N, device):
super(Quantizer, self).__init__()
centroids = torch.randn(N)
centroids, index = centroids.sort()
self.centroids = nn.Parameter(
centroids.clone().detach().to(device).requires_grad_(True)
)
Then, we can create an instance of this quantizer and set it in training mode, which allows for the gradients to accumulate.
quantizer = Quantizer(N, device)
quantizer.train()
quantizer.zero_grad()
Then the optimizer is defined using one of the following
optim = torch.optim.SGD(quantizer.parameters(), lr=1e-2, momentum=0)
# optim = torch.optim.SGD(quantizer.parameters(), lr=1e-2, momentum=0.9)
# optimizer = torch.Adam(quantizer.parameters(), lr=1e-2)
Finally, one step of gradient descent can be applied using one sample at index step of xs by following the below steps:
- Find the closest centroid to the sample while making sure we do not accumulate the gradients, for that the use of
with torch.no_grad():is essential, - Make sure the gradients are set to zero in
optim(or equivalently inquantizer.parameters()) by callingoptim.zero_grad(), - Compute the loss, in our case the distortion,
- Compute the gradients using
loss.backward(), - Apply the gradient descent step with
optim.step().
with torch.no_grad():
# Compute the vertices that separate the centroids
vertices = 0.5 * (quantizer.centroids[:-1] + quantizer.centroids[1:])
# Find the index of the centroid that is closest to each sample
index_closest_centroid = torch.sum(xs[step, None] >= vertices[None, :]).long()
# Set the gradients to zero
optim.zero_grad()
# Compute the loss
loss = 0.5 * (quantizer.centroids[index_closest_centroid] - xs[step])**2
# Compute the gradient
loss.backward()
# Apply one step of the gradient descent
optim.step()
Finally, I give the full implementation below. Concerning the optimizer choice, I chose SGD without momentum for my tests / benchmark in order to exactly replicate the results obtained in clvq_method_dim_1_pytorch with lr=1e-2.
def clvq_method_dim_1_pytorch_autograd(N: int, M: int, num_epochs: int, device: str, seed: int = 0):
"""
Apply `nbr_iter` iterations of the Competitive Learning Vector Quantization algorithm in order to build an optimal
quantizer of size `N` for a Gaussian random variable. This implementation is done using torch.
N: number of centroids
M: number of samples to generate
num_epochs: number of epochs of fixed point search
device: device on which perform the computations: "cuda" or "cpu"
seed: numpy seed for reproducibility
Returns: centroids, probabilities associated to each centroid and distortion
"""
torch.manual_seed(seed=seed) # Set seed in order to be able to reproduce the results
# Draw M samples of gaussian variable
xs = torch.randn(M)
xs = xs.to(device) # send samples to correct device
quantizer = Quantizer(N, device)
quantizer.train()
quantizer.zero_grad()
optim = torch.optim.SGD(quantizer.parameters(), lr=1e-2, momentum=0)
# optim = torch.optim.SGD(quantizer.parameters(), lr=1e-2, momentum=0.9)
# optim = torch.optim.AdamW(quantizer.parameters(), lr=1e-2)
with trange(num_epochs, desc=f'CLVQ method - N: {N} - M: {M} - seed: {seed} (pytorch autograd: {device})') as epochs:
for epoch in epochs:
for step in range(M):
with torch.no_grad():
# Compute the vertices that separate the centroids
vertices = 0.5 * (quantizer.centroids[:-1] + quantizer.centroids[1:])
# Find the index of the centroid that is closest to each sample
index_closest_centroid = torch.sum(xs[step, None] >= vertices[None, :]).long()
# Set the gradients to zero
optim.zero_grad()
# Compute the loss
loss = 0.5 * (quantizer.centroids[index_closest_centroid] - xs[step])**2
# Compute the gradient
loss.backward()
# Apply one step of the gradient descent
optim.step()
quantizer.eval()
probabilities, distortion = get_probabilities_and_distortion(quantizer.centroids, xs)
return quantizer.centroids.clone().detach().to('cpu').numpy(), probabilities, distortion
Numerical experiments
Now, I compare the average elapsed time of an epoch of the previous three algorithms. I analyze the computation time of the algorithms for different sample size (M), grid size (N) and devices for the PyTorch implementation.
All the tests were conducted on Google Colab with 16 Go of RAM and a NVIDIA T4 GPU.
Remark
When comparing numerical methods for building an optimal quantizer, it’s important to note that using the same seed and gradient descent parameters in both the numpy and PyTorch implementations does not result in identical centroids and probabilities. This is due to the fact that Numpy and PyTorch use different random generators, resulting in slightly different initial random samples. In order to replicate the results exactly across all algorithms, it is necessary to use a single random generator for all methods and set the same seed at the beginning of each method.
However, those differences have no impact when benchmarking each method and looking at the average time of an epoch.
In order to reproduce the benchmark’s result, you can use the script benchmark/run_clvq.py in the GitHub repository montest/stochastic-methods-optimal-quantization.
For different values of M, in the top graph, I display for each method, the average time of an iteration for several values of N.
In the bottom graph, I plot, for each N, the ratio between the average time for each method and the average time spent by the numpy implementation running on cpu.








Conclusion
In the previous graphs, we can notice that the implementation in Pytorch mimicking numpy is a lot slower compared to the one on Numpy (around 4 to 8 times slower on cpu and 10 to 20 times slower on cuda). This is maybe because of the batch size equal to one which does not fully take advantage of Pytorch. Indeed, we apply the gradient descent with one sample at the time. It would be of interest to test with bigger batch size. Moreover, the pytorch implementation allows us to have access to all the optimizers already implemented in Pytorch and choosing one that would speed up the convergence. Moreover, this code implementation in Pytorch is probably not optimal and one can find optimized version of it, lowering the ratios.
Concerning the Pytorch implementation using autograd, the ratios are even bigger up to 70 times slower when running on cuda and up to 30 on cpu. But those results are to be expected. Indeed, when using autograd, we perform more computations by computing the loss then differentiating with respect to all the centroids. While, when we compute directly the gradient and apply by hand the gradient descent, we compute if directly for the centroid which is the closest to the sample. Hence, again, it would be interesting to study the behavior of the autograd method with bigger batch size (with values $>1$) and see if the automatic differentiation can be of interest.
To conclude, in this case, the pytorch implementation with autograd is not interesting from on optimization point of view but it opens the door to more possibilities and applications, e.g. in the deterministic case in order to avoid computing the gradient by hand or in higher dimension. Hence, stay tuned for more updates 😃.

 In this post, I present a PyTorch implementation of the stochastic version of the Lloyd algorithm, aka K-means, in order to build Optimal Quantizers of $X$, a random variable of dimension one. The use of PyTorch allows me perform all the numerical computations on GPU and drastically increase the speed of the algorithm.
In this post, I present a PyTorch implementation of the stochastic version of the Lloyd algorithm, aka K-means, in order to build Optimal Quantizers of $X$, a random variable of dimension one. The use of PyTorch allows me perform all the numerical computations on GPU and drastically increase the speed of the algorithm.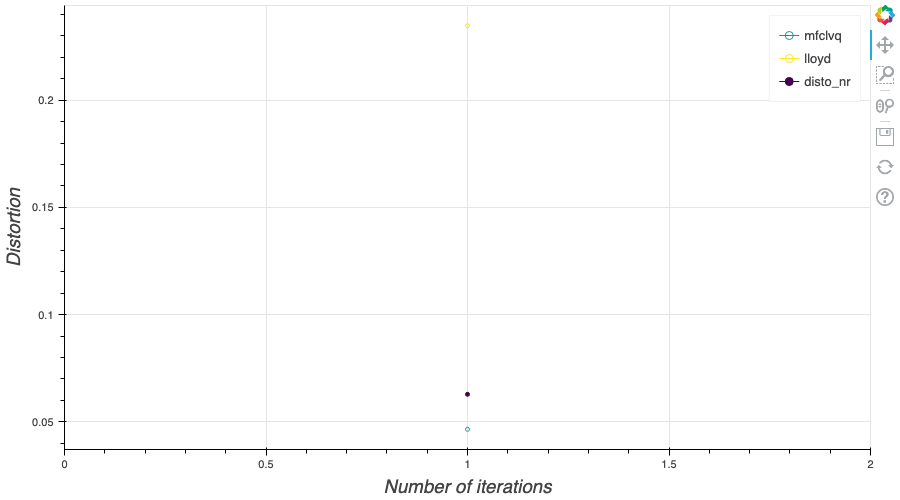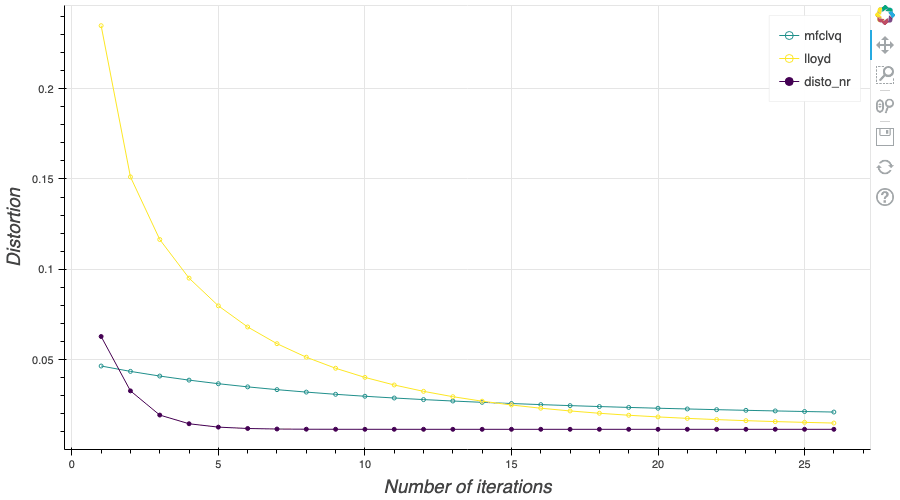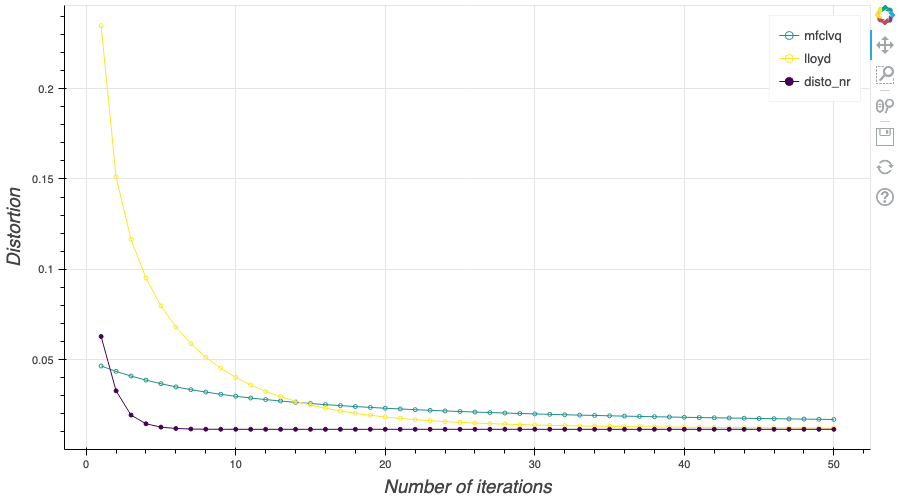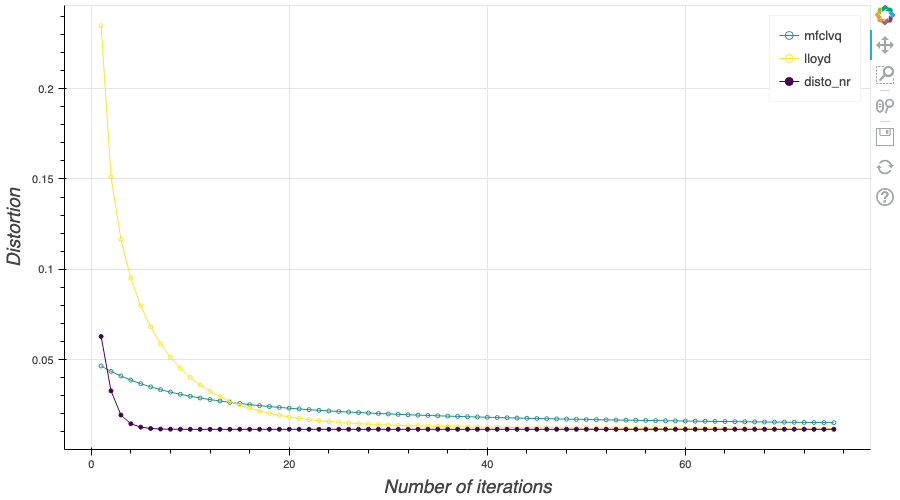 In my previous blog post, I detailed the methods used to build an optimal Voronoï quantizer of random vectors \(X\) whatever the dimension \(d\). In this post, I will focus on real valued random variables and present faster methods for dimension $1$.
In my previous blog post, I detailed the methods used to build an optimal Voronoï quantizer of random vectors \(X\) whatever the dimension \(d\). In this post, I will focus on real valued random variables and present faster methods for dimension $1$. In this post, I remind what is quadratic optimal quantizations. Then, I explain the two algorithms that were first devised in order to build an optimal quantization of a random vector $X$, namely: the fixed-point search called Lloyd method and the stochastic gradient descent known as Competitive Learning Vector Quantization (CLVQ).
In this post, I remind what is quadratic optimal quantizations. Then, I explain the two algorithms that were first devised in order to build an optimal quantization of a random vector $X$, namely: the fixed-point search called Lloyd method and the stochastic gradient descent known as Competitive Learning Vector Quantization (CLVQ).