Page Not Found
Page not found. Your pixels are in another canvas.
Sitemap
A list of all the posts and pages found on the site. For you robots out there is an XML version available for digesting as well.
Pages
About me
About me
Posts
Optimal Quantization with PyTorch - Part 2: Implementation of Stochastic Gradient Descent
Published:
In this post, I present several PyTorch implementations of the Competitive Learning Vector Quantization algorithm (CLVQ) in order to build Optimal Quantizers of $X$, a random variable of dimension one. In my previous blog post, the use of PyTorch for Lloyd allowed me to perform all the numerical computations on GPU and drastically increase the speed of the algorithm. However, in this article, we do not observe the same behavior, this pytorch implementation is slower than the numpy one. Moreover, I also take advantage of the autograd implementation in PyTorch allowing me to make use of all the optimizers in torch.optim. Again, this implementation does not speed up the optimization (on the contrary) but it opens the door to other use of the autograd algorithm with other methods (e.g. in the deterministic case).
All explanations are accompanied by some code examples in Python and is available in the following Github repository: montest/stochastic-methods-optimal-quantization.
Optimal Quantization with PyTorch - Part 1: Implementation of Stochastic Lloyd Method
Published:
In this post, I present a PyTorch implementation of the stochastic version of the Lloyd algorithm, aka K-means, in order to build Optimal Quantizers of $X$, a random variable of dimension one. The use of PyTorch allows me perform all the numerical computations on GPU and drastically increase the speed of the algorithm.
All explanations are accompanied by some code examples in Python and is available in the following Github repository: montest/stochastic-methods-optimal-quantization.
Deterministic Numerical Methods for Optimal Voronoï Quantization: The one-dimensional case
Published:
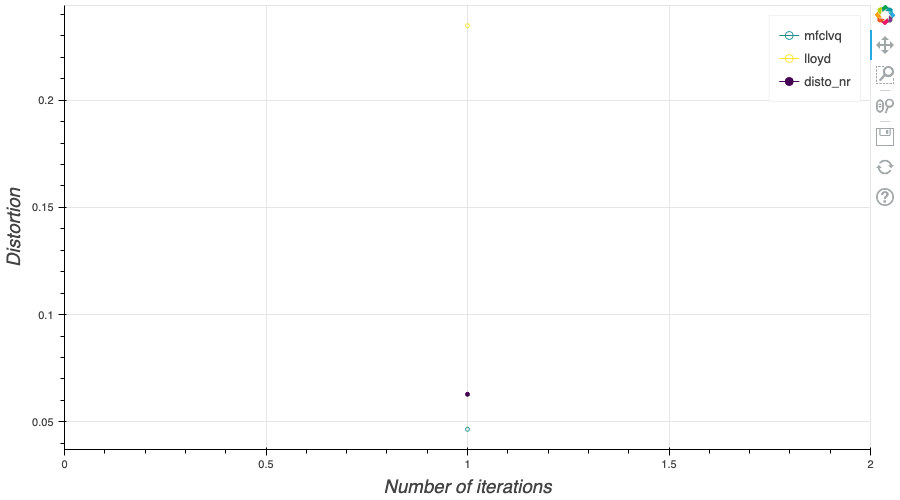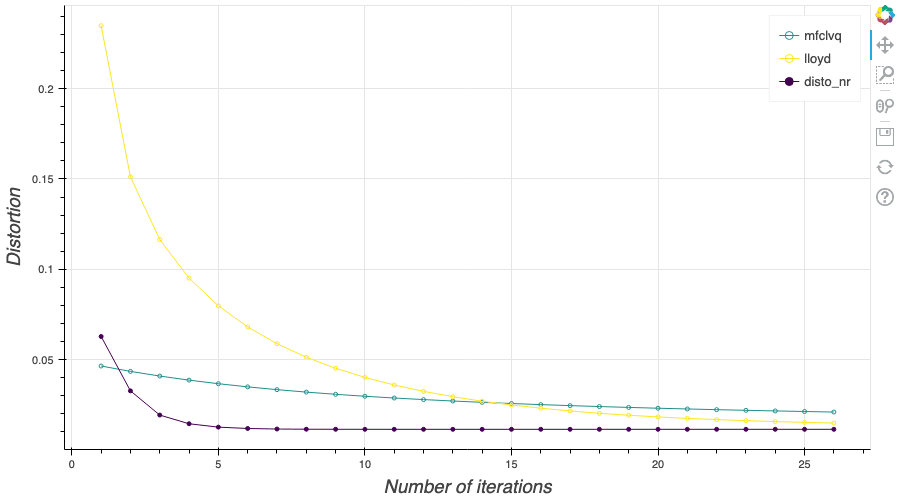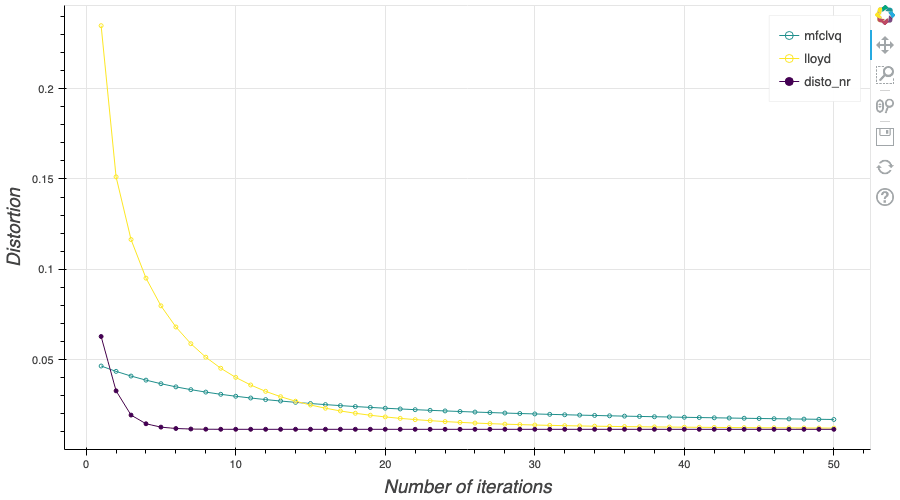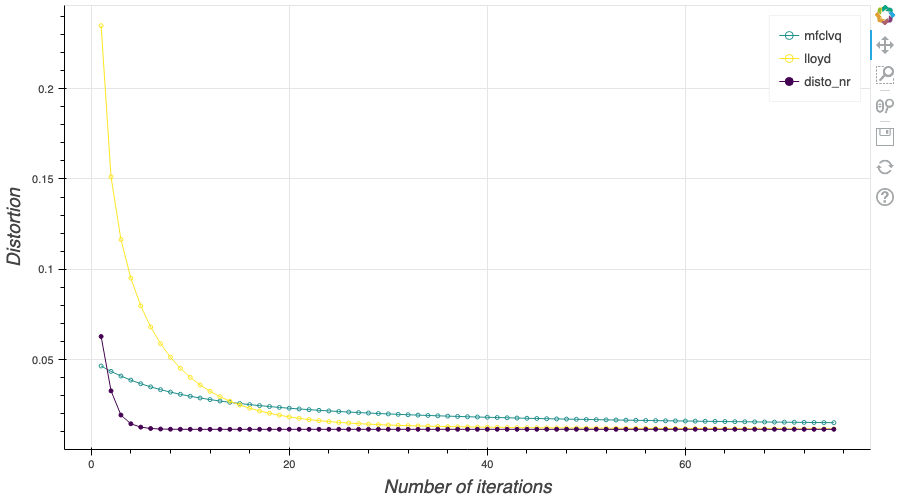In my previous blog post, I detailed the methods used to build an optimal Voronoï quantizer of random vectors \(X\) whatever the dimension \(d\). In this post, I will focus on real valued random variables and present faster methods for dimension $1$.
All the code presented in this blog post is available in the following Github repository: montest/deterministic-methods-optimal-quantization.
Stochastic Numerical Methods for Optimal Voronoï Quantization
Published:
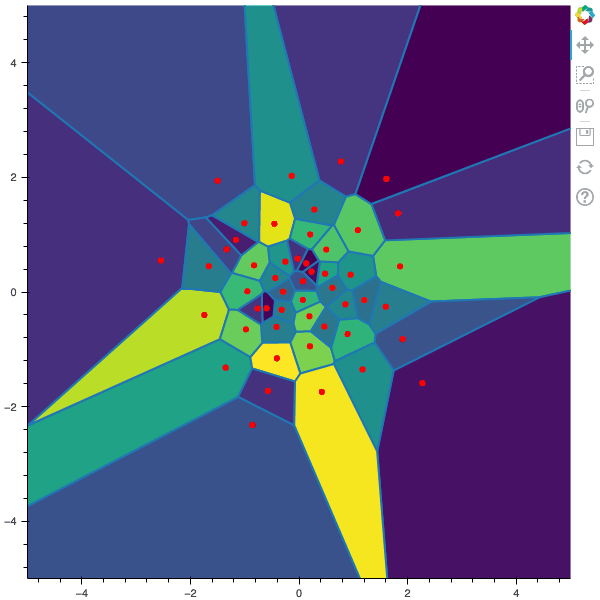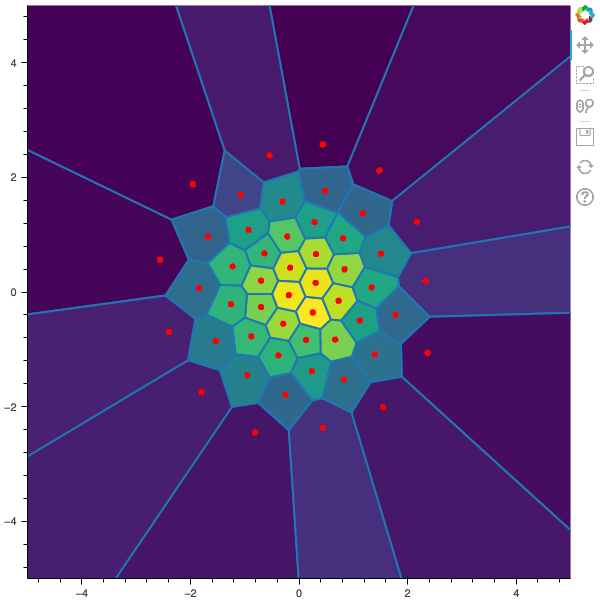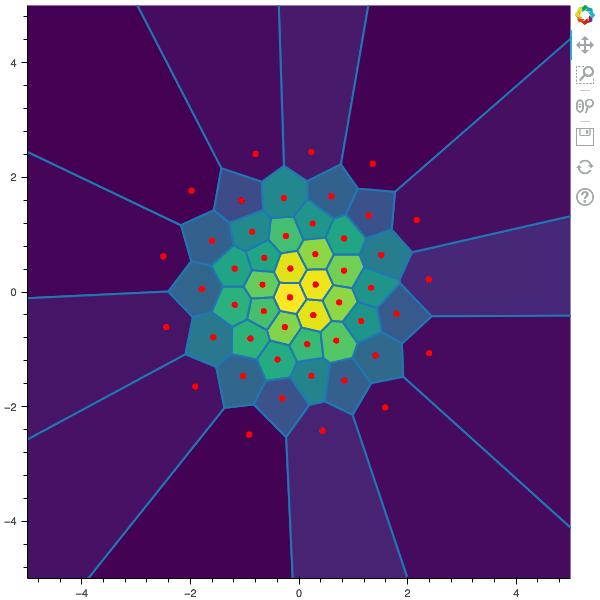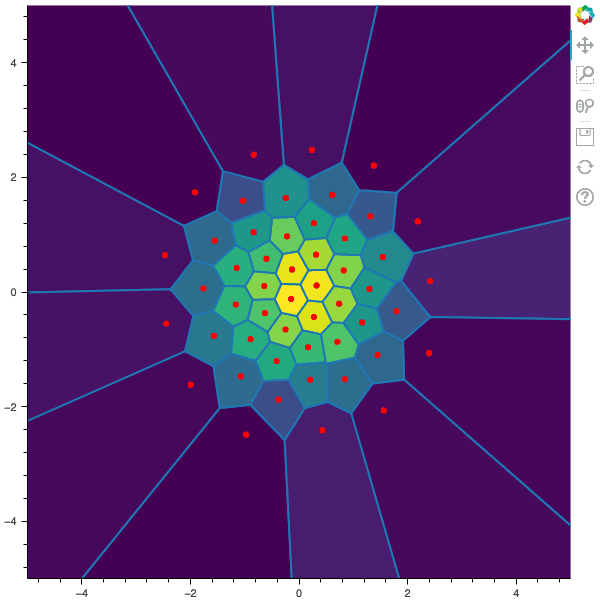In this post, I remind what is quadratic optimal quantizations. Then, I explain the two algorithms that were first devised in order to build an optimal quantization of a random vector $X$, namely: the fixed-point search called Lloyd method and the stochastic gradient descent known as Competitive Learning Vector Quantization (CLVQ).
All explanations are accompanied by some code examples in Python and is available in the following Github repository: montest/stochastic-methods-optimal-quantization.
publications
New Weak Error bounds and expansions for Optimal Quantization
Published in Journal of Computational and Applied Mathematics, 2019
We introduce new error bounds in dimension one for optimal quantization based cubature formula for a class of function that allows us to reach weak error of order two. This new results use deeply the local behaviors of optimal quantizers as well as Lr-Ls mismatch distortion results.
Download here
Quantization-based Bermudan option pricing in the $FX$ world
Published in Journal of Computational Finance, 2019
This paper proposes two numerical solution based on Product Optimal Quantization for the pricing of Foreign Exchange (FX) linked long term Bermudan options e.g. Bermudan Power Reverse Dual Currency options, where we take into account stochastic domestic and foreign interest rates on top of stochastic FX rate, hence we consider a 3-factor model.
Download here
Stationary Heston model: Calibration and Pricing of exotics using Product Recursive Quantization
Published in Quantitative Finance, 2020
A major drawback of the Standard Heston model is that its implied volatility surface does not produce a steep enough smile when looking at short maturities. For that reason, we introduce the Stationary Heston model where we replace the deterministic initial condition of the volatility by its invariant measure and show, based on calibrated parameters, that this model produce a steeper smile for short maturities than the Standard Heston model. We also present numerical solution based on Product Recursive Quantization for the evaluation of exotic options (Bermudan and Barrier options).
Download here
research
talks
New weak error bounds and expansions for optimal quantization with Applications
Published:
I present new weak error bounds and expansion in dimension one for optimal quantization-based cubature formula for different classes of functions, such that piecewise affine functions, Lipschitz convex functions or differentiable function with piecewise-defined locally Lipschitz or α-Hölder derivatives. This new results rest on the local behaviors of optimal quantizers, the Lr-Ls distribution mismatch problem and Zador’s Theorem. This new expansion supports the definition of a Richardson-Romberg extrapolation yielding a better rate of convergence for the cubature formula. An extension of this expansion is then proposed in higher dimension for the first time. We then propose a novel variance reduction method for Monte Carlo estimators, based on one dimensional optimal quantizers.
Download here
Tackling Stationary and Randomized Heston Models using Quantization
Published:
I present a work (still in progress) where we introduce a randomized/stationary version of the well known Heston model. This model allows us to produce steeper implied volatilities for short maturities options. We propose numerical solutions based on optimal quantization for the pricing of European, Bermudan and Barrier options.
Download here
Stationary Heston model: Calibration and Pricing of exotics using Optimal Quantization
Published:
A major drawback of the Standard Heston model is that its implied volatility surface does not produce a steep enough smile when looking short maturities. For that reason, we introduce the Stationary Heston model where we replace the deterministic initial condition of the volatility by its invariant measure and show, based on calibrated parameters, that this model produce a steeper smile for short maturities than the standard Heston model. We also present numerical solution based on Product Recursive Quantization for the evaluation of exotic options (Bermudan and Barrier options).
Download here
Stationary Heston model: Calibration and Pricing of exotics using Product Recursive Quantization
Published:
A major drawback of the Standard Heston model is that its implied volatility surface does not produce a steep enough smile when looking short maturities. For that reason, we introduce the Stationary Heston model where we replace the deterministic initial condition of the volatility by its invariant measure and show, based on calibrated parameters, that this model produce a steeper smile for short maturities than the standard Heston model. We also present numerical solution based on Product Recursive Quantization for the evaluation of exotic options (Bermudan and Barrier options).
Download here